Forum

Välkommen gäst

Sök | Aktiva konversationer | Logga in | Registrera dig

Sök

Postad av
Meddelanden

2 Sidor 12>

Resultat
Konversation: Avstängd som volontär/läxhjälpare vid Mattecentrum i Lund
Mikael	Postad: den 18 oktober 2012 18:47:24
	Jag har tyvärr blivit avstängd som volontär/läxhjälpare vid Mattecentrum i Lund. Så här förklarade jag det för de andra volontärerna. Hej Volontärer på Mattecentrum i Lund, jag skrev följande två kommentarer på den slutna Facebook-gruppen för enbart volontärer på Mattecentrum i Lund samt skickade utdrag av citaten till Mattecentrum centralt. Jag fick igår ett e-brev från Sara Cedell om att jag var avstängd som volontär och samtidigt tog Johan Wendt (ordf) bort mig som vän på Facebook. Det är dock Martin Aalto [projektledare vid Mattecentrum i Lund] som är ansvarig för beslutet. Jag har ju värvat alla medlemmar till Mattecentrum med motiveringen att det är en demokratisk organisation men så här beter sig inte en demokratisk organisation. Det verkar otroligt att man kan bli avstängd som volontär baserat på frågor om ett nytt avtal och några av er kommer säkert tro att något annat måste ligga bakom, men ni har mitt ord som matematiker att detta var allt jag gjorde. Dock kan det ju inte uteslutas att Martin Aalto eller Mattecentrums ledning har något annat emot mig, men det har jag inte hört något om tidigare. För bara få dagar sedan gillade både Johan och Martin ett inlägg av mig på Facebook. Det är trist att det blir svårare för mig att ge läxhjälp och jag tyckte också de av er jag träffade var trevliga och kompetenta. Jag har varit volontär sedan 2009 och var den förste projektledaren i Lund tills jag fick jobb på avlägsen ort men senare återkom jag som vanlig volontär. Jag anser att ni bör låta en advokat granska volontärskontraktet innan ni eventuellt skriver på det. Det finns risk för skadestånd baserat på godtycklig rättsskipning. Jag har aldrig sett något liknande kontrakt tidigare. Jag tycker Martin Aalto borde avsättas som ordförande i Lund p.g.a. bristande omdöme och civilkurage och ersättas med någon som inte vill stänga av volontärer baserat på några frågor och vissa faktabaserade påståenden. För min del får Martin Aalto gärna fortsätta som volontär. De två Facebook-kommentarerna: "Detta är kanske första tecknet på att Mattecentrum håller på att förvandlas till en sekt. De vill att vi skall skriva på ett kontrakt med namnteckning, namnförtydligande och ort och datum men vi är inte anställda. Ett vanligt kontrakt kan man visa för facket och så kan de uttala sig om det är vettigt. Detta kontrakt kan jag ej ta till facket eftersom det inte är ett anställningskontrakt. Det blir dyrare att ta det till en advokat. Jag antar att man måste sluta som läxhjälpare i Mattecentrum om man inte skriver på kontraktet. Om det inte är något straff för att bryta mot kontraktet, varför vill de då att vi skall skriva på det? Om det är något straff för att bryta mot kontraktet, hur stort är det? Var lagras kontrakten? Om jag tvingas att sluta på Mattecentrum för att jag inte har råd att reda ut konsekvenserna av kontraktet så startar jag min egen konkurrerande läxhjälpsorganisation inom Matematik och liknande. Den kommer inte kräva att icke-anställda skall skriva på kontrakt. Hur lagras kontrakten? Jag kommer fortfarande vara vanlig medlem i Mattecentrum och försöka rösta bort dem som föreslagit att icke-anställda läxhjälpare skall skriva på kontrakt. Det är inte innehållet i kontraktet jag är emot utan att det faktum att vi måste skriva på ett kontrakt utan att vara anställda. Om vi är en egen förening i Lund, vilket vi lär vara, och inte anställda av Stockholm så borde vi inte behöva skriva på kontrakt och skicka till Stockholm. Dessutom är det tvivelaktigt att lundamedlemmarnas pengar från Ungdomsstyrelsen förbrukas i Stockholm." "Jag undrar också vad som händer om man bryter mot kontraktet och vem som avgör att man bryter mot kontraktet. Jag vill helst inte skriva på några kontrakt i onödan. Jag anser att idén om kontrakt var dålig och skriver en motion till nästa årsmöte om att de skall avskaffas -- åtminstone för de volontärer som inte är anställda. Det är som sagt dyrt att utreda konsekvenserna av kontraktet när det inte är en del av ett anställningskontrakt eftersom man inte får hjälp av facket." Upprepning från en kommentar på Facebook i eftermiddag: P.g.a. enbart dessa två kommentarer i denna slutna grupp så anklagades jag för att sprida rykten och fick e-brev från Mattecentrum om att jag är avstängd från att vara volontär. Tydligen är det så att endast de som inte har kritiska åsikter om något relaterat till Mattecentrum får vara volontärer. Dock är det ju enbart Martin Aaltos beslut som är giltigt ty han är projektledare i Lund men han verkar tyvärr hålla med ledningen. Jag har varit volontär i Mattecentrum sedan 2009 och var den första projektledaren fram till våren 2010 då jag fick jobb i Karlskrona -- efter det återkom jag dock som volontär. Jag skall dock försöka få avstängningsbeslutet upphävt. Att Mattecentrum centralt just nu bevisligen är antidemokratiskt borde inte påverka oss. Vi skulle kunna döpa om föreningen i Lund och bilda vår egna utbrytarorganisation. Om ni är intresserade av detta så kan ni kontakta mig på mikaelb@df.lth.se. Jag tänker kvarstå som medlem i Mattecentrum och försöka reformera föreningen genom att skriva motioner och kandidera till poster. Möjligen blir jag även utsluten som medlem. Jag kommer också fortsätta att ge gratis läxhjälp till elever på gymnasienivå ca 2 h per vecka, men det blir ju svårare att organisera om man bara är en. Nu vet ju ni om att det är extremt lågt till tak i Mattecentrum, men det visste ju inte jag. Jag jobbar nu 40% som år 3-6 lärare i trä- och metallslöjd. Jag är ju fil. mag. (MSc) i fysik vid Lunds Universitet så det är ju ganska långt från min utbildning (jag har även Högskoleexamen i Matematik från LU) men jag är även intresserad av design och man får ta de jobb som finns på den krympande arbetsmarknaden. Jag studerar även apputveckling för Android och skall snart börja på en styr- och reglerkurs. Svar på inläggen nedan eftersom jag är blockerad från att svara men fortfarande kan redigera det ursprunliga inlägget: Jag postade även detta i Mattecentrums forum i gruppen Om Mattecentrum, men nu är jag blockerad från att skriva där. Henrik wrote: Jättedåligt av dej att spamma detta forum, Mikael. Starta en egen matteläxhjälp i stället för att sabba för oss andra. Jag tycker det är jättedåligt och antidemokratiskt av Henrik att skriva så här. Enligt svenska skolans värdegrund skall man uppfostras till att bli en demokratisk människa. Jag hade högre tankar om Henrik p.g.a. hans inlägg här. Att acceptera att en medvolontär stängs av på dessa grunder anser jag vara att bejaka de antidemokratiska krafterna. Det är väl lämpligt att man diskuterar avstängning p.g.a. åsikter om Mattecentrum i Mattecentrums forum. Jag anser att permanenta avstängningen av mig som volontär med motiveringen att jag sprider rykten baserat på de två kommentarerna i en sluten Facebook-grupp visar att Mattecentrum är en odemokratisk organisation som inte tillåter sina medlemmar att sprida åsikter och komma med tips om att man borde kontrollera ett avtal innan man skriver på det. Alltså borde Mattecentrum inte få lov att driva sin verksamhet i skolans lokaler eftersom organisationen inte delar svenska skolans värdegrund om att man t.ex. frimodigt skall få uttrycka sina åsikter. Man skall ju kunna säga sektvarning om en organisations påbud liknar de från en sekt. Det är ju inte lika lätt att starta en ny läxhjälpsorganisation nu än innan Mattecentrum fanns p.g.a. lokalbrist och konkurrens. (Lokalbristen bör dock lösas om kommunerna förljer reglerna om svenska skolans värdegrund och kastar ut Mattecentrum.) Jag tyckte idén om Mattecentrum var utmärkt och därför hoppade jag på som projektledare och volontär direkt när jag hörde talas om det via mitt fackförbund Naturvetarna 2009. Jag känner att den enda verksamhet jag uppskattar från centralt håll är detta forum och broschyrerna. Att ledningen kuskar land och rike runt och gör sig viktiga anser jag vara slöseri med pengar och flygbränsle. Jag brukar alltid låta mitt fack granska anställningsavtal innan jag skriver på dem, men eftersom detta inte är ett anställningsavtal så måste jag be en jurist reda ut konsekvenserna av att skriva på det och det blir dyrt. Dock finns det vissa möjligheter att få gratis juridisk rådgivning. Nu är ju detta en hypotetisk fråga eftersom jag är avstängd som volontär. Svar till Yngve #7: Du verkar fortfarande inte förstå att jag inte är emot reglerna. Jag har följt samma regler och fler sedan 1992 då jag först började jobba som gymnasielärare. Jag ställde frågor om kontraktet (du ser dem i sin helhet ovanför) och blev avstängd som volontär permanent utan möjlighet att överklaga. Jag fick visserligen svar på vissa av frågor i samma brev som avstängningsbrevet men då var jag redan avstängd som volontär. Förövrigt är avtalet oklart och enligt uppgift aldrig kontrollerat av en jurist, så möjligheten finns att det missbrukas. Bryr du dig inte om att Mattecentrum genom avstängningen av mig som volontär härmed har bevisat att den är en antidemokratisk förening? Det är detta debatten borde handla om.
Konversation: Skillnad mellan Matte 1 A resp B och C?
Mikael	Postad: den 26 augusti 2012 21:25:33
	Guest wrote: Hej! Vad är skillnaden mellan de olika varianterna av matte 1? Inför högskoleprovet står det att den teoretiska nivån är liktydig med matte 1, men som jag förstår förekommer matte 1 i olika varianter? Vilken motsvarar i så fall matten för det naturvetenskapliga programmet? Tacksam om någon kan upplysa mig : ) Matte 1c är för naturvetenskapliga-programmet, Matte 1b är för samhällsprogrammet och Matte 1a är för yrkesprogrammen. Kursplaner: http://matematik1c.se/ http://matematik1b.se/ http://matematik1a.se/ När det gäller att träna matte inför Högskoleprovet så kan man öva på de kvantitativa delarna på gamla högskoleprov. En strategi är att lösa dem långsamt och ganska fullständigt när man övar, men sedan på provet måste man korta ner lösningen och svara inom en viss tid i annat fall hinner man inte med slutet. Svårighetsgraden ökar inte med uppgiftsnumret så det kan finnas enkla uppgifter i slutet av provet. Man måste kunna enkel huvudräkning och överslagsräkning i annat fall tappar man en massa tid.
Konversation: Lösa 2:a- & 3:e-gradsekv., ekv.sys., determinanter & integraler på Android ZX81
Mikael	Postad: den 26 augusti 2012 20:31:38
	Jag tänkte bara tipsa om ett program jag upptäckte 1985 för ZX Spectrum som jag då portade till ZX81-BASIC. (Sinclair ZX81 var en tidig hemdator som kom ut 1981.) Det går att köra i ZX81-emulatorer t.ex. Zed Ex för Android (finns gratis på Google Play). Programmet klarar att numeriskt lösa/beräkna 2:a- & 3:e-gradsekvationer, ekvationssystem, matrisinverser, determinanter, integraler. En pedagogisk fördel är att programkoden kan studeras och redigeras i ZX81-emulatorn på t.ex. mobilen. En annan pedagogisk fördel är att programspråket ZX81-BASIC inte har några kraftfulla finesser utan programmet måste göra nästan allt själv. Programmet presenterades i en artikel i tidskriften Your Computer i Maj 1985 på s. 57 & 58. Programfilen som man skall ladda ner till sin emulator heter maths.p. Om man använder Zed Ex så bara lägger man filen någonstans i filsystemet och öppnar filen med meny & load. Jag har testat min portning av det ursprungliga programmet med exemplen från artikeln. (Artikeln innehåller ganska många tryckfel, men jag har även jämfört med http://www.wolframalpha.com/.) Här finns en listning av programmet Maths Master och en skärmdump: Förutom att porta program avsedda för andra datorer så utvecklade jag även en hel del helt egna program t.ex. 2D-flygspelet Mirage (1982) och glosträningsprogrammet Glosa (1982), se min allmänna ZX81 App Store.
Konversation: Modellering?!
Mikael	Postad: den 19 maj 2012 16:17:21
	Modellering är ett ganska vitt begrepp. Vilken mattebok har du? Vad heter kapitlet? Vilken modell på grafräknaren har du?
Konversation: Sannolikhet
Mikael	Postad: den 19 maj 2012 06:04:42
	Jag tänker mig ett binärt tal med 4 slumpmässigt valda siffror (0 och 1). Om klave=0 och krona=1 blir antalet kronor samma som siffersumman. Det finns 16 binära tal med 4 siffror, ty multiplikationsprincipen ger 2^4=16. a) Samtliga binära tal med siffersumman 2: 0011 0101 1001 0110 1010 1100 D.v.s. 6 stycken. Det är ganska lätt att hitta dem systematiskt, ty jag börjar med att sätta den högra siffran till 1 och sedan de övriga till 1 en i taget från höger till vänster. Sedan sätter jag den näst mest högra till 1 och gör på samma sätt. I denna uppgift blir antalet klave=2 när antalet krona=2 ty det är fyra kast. Sannolikheten blir alltså antalet binära tal med siffersumman 2 delat med totala antalet binära tal: 6/16=0,375. b) Då skall man hitta de binära tal med 4 siffror som har en siffersumma >= 2. 6 st. har siffersumman 2. Samtliga med siffersumman 3: 1110 1101 1011 0111 D.v.s. 4 st. Man har 0:an i de fyra möjliga positionerna och förövrigt 1:or. Samtliga med siffersumman 4: 1111 Antalet med siffersumman >=2: 6+4+1=11. Sannolikheten att antalet kronor är minst 2: 11/16=0,6875. Det finns möjligen någon smartare metod att lösa dessa problem. Man kan också lösa uppgiften med ett program (för i detta fall Texas Instruments TI-82 STATS/TI-83/TI-83 Plus/TI-84 Plus): PROGRAM:SINGLA4 :1000->N :0->K :For(I,1,N) :randInt(0,1,4)->L_1 :If sum(L_1)>=2 :K+1->K :End :K/N Vill man lösa uppgift a med detta program byter man '>=' mot '='.
Konversation: Till Louisa, Uppgift 5141: Brinntiden för lågenergilampor
Mikael	Postad: den 18 maj 2012 04:55:10
	Jag förstår din lösning Henrik. Jag hade den idén initialt (d.v.s. att hitta ett komplicerat uttryck med p lika med 0,95 och lösa ut p) men var lite ringrostig när det gällde kombinatorik. Nu har jag dock gjort din lösning mer exakt med wxMaxima (gratis och öppen källkod och finns till de flesta vanliga operativsystem): Code: binomial(12,2); 66 Du summerar sannolikheterna för P(0 trasiga), P(1 trasig), P(2 trasiga): Code: find_root(p^12+12(1-p)p^11+66(1-p)^2p^10-.95, p, 0, 1); 0.92812974445773 find_root(cdf_normal(x,10000,600)-(1-%),x,8000,12000); 9122.798469979023 %/1461; 6.2442152429699 "%" betyder samma som Ans d.v.s. senaste svaret. Min simulering (lösning 1) får ett högre värde eftersom jag tar reda på tiden precis innan den 3:e lampan går sönder. Min lösning 2 får ett ännu högre värde eftersom jag antar att det finns ett oändligt antal lampor men där andelen trasiga skall vara lägre än 3/12. Jag löste även problemet för Texas Instruments TI-84 Plus med en TI-83-emulator: Code: solve(X^12+12(1-X)X^11+66(1-X)^2*X^10-.95, X, .5) .9281297445 solve(normalcdf(-1E99,X,10000,600)-(1-Ans),X,10000) 9122.798305 Ans/1461 6.24421513
Konversation: Matlab/Octave/Addi för Android & GNU R
Mikael	Postad: den 18 maj 2012 02:00:48
	Den senaste versionen av Addi är så stor (20 MB) att den inte går att installera på min Android-surfplatta. Dock kan man hämta ner äldre, betydligt mindre versioner från: http://code.google.com/p/addi/downloads/list.
Konversation: Standardavvikelse med TI 82 STATS
Mikael	Postad: den 18 maj 2012 01:20:21
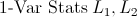
	Du trycker på [1-Var Stats (via menyer)] [2nd] [L1 (vid 1)] [,] [2nd] [L2 (vid 2)] Raden ser ut så här innen du trycker [Enter]: $\textup{1-Var Stats}\: L_1,L_2$
Konversation: Standardavvikelse med TI 82 STATS
Mikael	Postad: den 17 maj 2012 17:43:10
	Har du skrivit: Code: 1-Var Stats L_1,L_2 d.v.s. med två list-argument och komma emellan? Om jag tömmer L_2 och kör ovanstående så får jag ett felmeddelande: "ERR:DIM MISMATCH". Något annat hade jag inte förväntat mig i det fallet.
Konversation: Standardavvikelse med TI 82 STATS
Mikael	Postad: den 17 maj 2012 16:32:38
	När det gäller din fråga om TI-82 STATS (nästan identisk programvarumässigt med TI-83) så kan man ha värdena i lista L_1 och motsvarande frekvenser (d.v.s. antal värden) i lista L_2. Sedan använder man den vanliga proceduren med listorna som argument: 1-Var Stats L_1,L_2 Man kan se att man gjort rätt eftersom n=totala antalet värden, d.v.s. summan av L_2: sum(L_2)
Konversation: Till Louisa, Uppgift 5141: Brinntiden för lågenergilampor
Mikael	Postad: den 17 maj 2012 15:59:51
	Uppgift 5141 (i okänd Ma2c-bok): Brinntiden för en viss typ av lågenergilampor uppges till 10000 timmar med standardavvikelsen 600 timmar. Ett år bytte man till sådana lampor i 12 gatlyktor längs en vägsträcka. Man räknade med att lyktorna är tända 8 timmar/dygn under halva året. Efter hur många år måste man byta lampor om man vill vara någorlunda säker på att högst två lampor gått sönder? Antal timmar per år: 8 h/dag i ett halvår motsvarar 4 h/dag under 1 år. 1 år = 365.25 dag. 4 h/dag * 365.25 dag/år = 1461 h/år. Man räknar ut tiden i lys-timmar det tar i genomsnitt för 3 lampor att gå sönder och omvandlar sedan till år där man tagit hänsyn till att lamporna inte är på hela tiden (d.v.s. lys-timmar/1461). Tiden i år avrundas neråt, ty man vill vara säker på att ej fler än två lampor gått sönder. Andledningen till att man tar reda på när 3 lampor gått sönder är att man vill ha tiden precis innan den 3:e lampan gått sönder. Först kommer en lösningsmetod med program som ej är ett krav att förstå i Matematik 2c -- dock kan programmet underlätta förståelsen av uppgiften och lösning 2. Lösning 1: Jag skrev ett program för TI-84 Plus (som även fungerar på TI-82 STATS/TI-83/TI-83 Plus) som simulerar ett experiment 1000 gånger och beräknar medelvärdet för när den 3:e lampan går sönder. Funktionen randNorm ger en lista med 12 normalfördelade värden med det angivna medelvärdet och den angivna standardavvikelsen. Listan sorteras i stigande ordning och det 3:e värdet läggs till en summa. När man gjort experimentet 1000 gånger så beräknar man medelvärdet och det visas. (I programmet nedan gäller att "->" betyder STO-pilen och "L_1" betyder lista 1, d.v.s. [2nd] [L1].) PROGRAM:LAMPS :1000->N :0->S :For(I,1,N) :randNorm(10000,600,12)->L_1 :SortA(L_1) :S+L_1(3)->S :End :S/N 9525.23 (Varierar slumpmässigt, men ligger nära detta värde.) Ans/1461 6.52 Lösning 2: En alternativ metod som bygger mer på vad ni kan i Ma2c är att man använder normalfördelningen. Ytan under kurvan är 1. Till vänster om ett x-värde vill man ha 3/12=25% av utfallen. Anledningen till detta är att när 3 av 12 lampor gått sönder så har precis för många gått sönder. (Jag tänkte ut detta genom att tänka på att man kastar en boll en viss längd i stället för att tänka på tid -- då vill man att 25% av utfallen skall hamna närmare än en viss punkt.) Jag har tyvärr ej er kursbok och vet ej vilka tabeller ni har men grafräknaren TI-84 Plus m.fl. klarar detta. Man löser en ekvation. (I uttrycket nedan gäller att "E" betyder [2nd] [EE] och "normalcdf" betyder "Normal Cumulative Distribution Function" och det sista 10000 är gissningen på lösning som solve-funktionen behöver. Funktionen solve hittar man endast i CATALOG-listan. Funktionen solve klarar bara att hitta nollställen så därför tar man normalcdf()-3/12=0 i stället för normalcdf()=3/12.) solve(normalcdf(-1E99,X,10000,600)-3/12,X,10000) 9595.306285 Ans/1461 6.567629216 D.v.s. ca 6.5 år tar det för de 3 första lamporna att gå sönder. Därför bör man byta lamporna efter 6 år. Alla grafräknarens funktioner kan slås upp i manualen som finns på: http://education.ti.com/calculators/downloads/US/Guidebooks/Search/Results?cp=17 Naturligtvis kan man även lösa denna uppgift med CASIO:s grafräknare men jag vet att eleven har en TI-84 Plus. När det gäller livslängder, som det här handlar om, skall man egentligen inte använda normalfördelningen utan en annan fördelning men i denna uppgift förutsätter de att man bara kan normalfördelningen. Är denna lösning oklar så får någon annan gärna förtydliga.
Konversation: Grafräknarappar ritar riktningsfält f differentialekvationer
Mikael	Postad: den 5 maj 2012 06:25:43
	Jag hittade en mattelärares hemsida där ovanstående program redan fanns för nedladdning och med manualer, men det nya ovan är att det finns listningar och körexempel med differentialekvationen dy/dx=x+y samt versioner av apparna för gamla TI-82 (som många fortfarande har och som lär fungera i många år än ty jag har en TI-57 från 1977 som fortfarande fungerar bra och TI-82 kom ut 1993.) Här är hemsidan jag talar om: http://www.bjornjonsson.se/ti8xprogram.html. Sök efter Differentialekvationer på den. Det är i alla fall en nyttig övning att knappa in några små program ty man minns dem bättre och kan lättare analysera hur de fungerar.
Konversation: Grafräknarappar ritar riktningsfält f differentialekvationer
Mikael	Postad: den 4 maj 2012 19:16:56
	I läroboken Matematik 4000 Kurs E Blå s. 199 finns tre små appar/program på mindre än 30 rader för Texas Instruments (TI) grafräknare (TI-83, TI-82 STATS, TI-83 Plus & TI-84 Plus) som jag knappade in och dessutom översatte till TI-82. Jag tänkte att detta kunde vara till hjälp om någon behöver appar för differentialekvationer till grafräknare och kör fast när det gäller att skriva in dem. Det finns ju även utmärkta Casio grafräknare men jag har ännu inte hunnit översätta till dem än. Programmen i bilderna är till TI-83 o.s.v. - notera att TI-82 STATS är identisk med med TI-83 och ej så lik TI-82. Man behöver inte skriva in dem utan kan hämta ner dem här. Dock är det lärorikt att knappa in dem men som en nödlösning finns de här i gruppfiler: DIFF4000.83G DIFF4000.82G Jag använde TI:s intergrerade utvecklingsmiljö i Windows 2000 för att knappa in apparna (fungerar även i Linux med Wine). Dock gjorde jag Runge-Kuttas metod-programmet direkt på miniräknaren genom att klistra in Euler-programmet med RCL prgmDIFFEU och sedan modifiera det i miniräknaren. Casio har en liknande utvecklingsmiljö för Windows men har bättre redigeringsmöjligheter på räknaren. När jag jämför grafräknares funktioner och användbarhet så jämför jag räknare i samma prisklass.
Konversation: Var finns Nationella Provet i Matematik & formelbladen?
Mikael	Postad: den 2 maj 2012 05:38:21
	Föreningens webbplats http://Matteboken.se/lektioner/ladda-ner saknar vissa nysläppta prov och formelblad (och jag har rapporterat detta) – dock har Matteboken vissa unika övningsprov inför kurserna Matematik 1 & 2. Här finna alla gamla offentliga nationella prov för Matematik A-E: http://www.edusci.umu.se/np-pb/np/tidigare-prov/. Formelblad för Matematik 1-2: http://www.edusci.umu.se/np-pb/np-2-4/formelblad/. Nationella prov för matematik i grundskolan: http://www.prim.su.se/matematik/tidigare_9.html . Eleverna verkar mest syssla med de senaste proven.
Konversation: Formelblad för Matte 2/Matematik 2
Mikael	Postad: den 21 april 2012 03:06:46
	Jag har hittat formelbladet "FORMLER TILL NATIONELLT PROV MATEMATIK KURS 2" på http://www.edusci.umu.se/np-pb/np-2-4/formelblad/. Detta borde nog även läggas till i http://matteboken.se/lektioner/ladda-ne ... gymnasiet/.
Konversation: Matlab/Octave/Addi för Android & GNU R
Mikael	Postad: den 7 april 2012 17:15:03
	Jo, man kan verkligen köra ett Matlab™-liknande program gratis i sin mobil eller surfplatta med Android OS utan att behöva vara uppkopplad.
Konversation: Matlab/Octave/Addi för Android & GNU R
Mikael	Postad: den 6 april 2012 04:31:37
	Jag upptäckte att det finns Matlab/Octave för Android -- det heter Addi och AddiPlot: http://www.appbrain.com/app/addi/com.addi https://play.google.com/store/apps/details?id=com.addi För att öppna skript och funktioner behöver man ytterligare ett program (en filhanterare) men det installerar man när man behöver det. Både Addi och filhanteraren har App2SD så de tar inte stor plats på interna flash-minnet. Addi är väldigt lättanvänt på Android eftersom kommandoraden gissar vad man skriver och föreslår de orden att klicka på (s.k. IntelliSense). En nackdel med Addi är att historiken inte verkar fungera eftersom man inte har pilknappar. När man installerat Addi och AddiPlot på Androiden kan man prova att skriva in detta i Addi och trycka på Enter: x=[0:0.1:2*pi];y=sin(x);plot(x,y) Man får då upp en sinuskurva. Jag har använt Matlab på kurser i numerisk analys, beräkningsprogrammering samt i exjobbet och även senare på jobb. Dock har jag mest använt Octave som är en gratis och öppen källkods Matlab-klon efter 2004. Addi är baserat på JMathLib som förmodligen är baserat på Octave. Programspråket i Matlab/Octave/Addi är i stort sett BASIC. Jag har en bok om Matlab och en om Octave och fler finns att låna på bibliotek. Dessutom finns min Octave-bok online fast i nyare och större upplaga: http://www.gnu.org/software/octave/doc/interpreter/. Octave finns även till Windows: http://octave.sourceforge.net/. Jag har även en laglig Matlab 5 för Windows som ej behöver licensserver. Jag har dock inte så mycket tid att ägna åt Addi just nu eftersom jag lär mig andra saker, t.ex. CAD-kurs på LTH (Creo Parametric) och R. R verkar ha blivit populärt på sistone -- t.ex. finns det en hel del jobb i Region Skåne och på Lunds universitet som kräver R. Det är ett system med ett Scheme/LISP-liknande programspråk och med många statistiska funktioner. Det är en konkurrent till Matlab/Octave och diverse speciella statistikprogram som SAS och SPSS. R är öppen källkod och jag tycker det är bra att offentliga sektorn övergår till det. Mer om R finns på: http://en.wikipedia.org/wiki/R_%28progr ... anguage%29 -- där finns bl.a. ett spektakulärt exempel med en animerad Mandelbrot-figur. Man kan installera det i Ubuntu Linux med: sudo apt-get install r-base Möjligen kan man behöva installera extra paket senare. R finns även för Mac OS X och Windows men de versionerna har jag ännu inte provat. Jag har dock provat R för Linux i Windows 2000 med Cygwin http://www.cygwin.com/. Man startar en webbserver och webbläsare med dokumentation med R-kommandot: help.start() Det verkar som om webbservern avslutas när man avslutar R. Webbservern fungerar inte i Cygwin. I webbläsaren kan man leta sig fram till "An Introduction to R" /doc/manual/R-intro.html (som även kan hittas på webben) finns en nybörjarbok som även finns som tryckt bok och pdf. En fördel med att använda den inbyggda webbläsarens version är att den är till exakt samma version av R som man kör, vilket underlättar lärandet. Man avslutar med R-kommandot: q()
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 3 april 2012 09:43:10
	Nu har jag fått besked från Högskoleprovet: Det är fel i facit för uppgift 18 på provpass 5. Ett nytt facit kommer att publiceras. Rätt svar på uppgiften är D. :D
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 2 april 2012 14:44:58
	Jag har bara fått svar från Högskoleprovet att de undersöker saken.
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 2 april 2012 14:41:53
	Tagran har bara räknat på fallet där vinkel C är trubbig men enligt konventionerna för provet (som man fick i ett häfte på provet) och som jag har länkat till så får man inte antaga att vinklar som ej är angivna är trubbiga även om just den konkreta figuren har en trubbig vinkel – de kan alltså lika gärna vara spetsiga. Bägge figurerna nedan uppfyller beskrivningen i uppgiften men de leder till olika svar: A eller B, därför är D rätt. Code: B \| \| \| \| C \| \| \| \| +--+ A D /\| C / \| \|B \| +--+ A D Tyvärr fungerade inte ickeproportionell text helt bra.
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 2 april 2012 01:52:29
	Rita figuren med spetsig vinkel vid C så ser du att tecknet framför kvadratroten blir minus och då blir sidan AB
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 1 april 2012 02:19:05
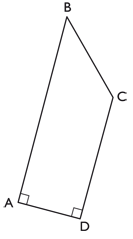
	Här är uppgiften för dem som inte vill leta upp den på studera.nu: 18. I fyrhörningen ABCD är vinklarna DAB och CDA räta. Längden av sidan BC är 3 cm, längden av sidan CD är 4 cm och längden av sidan AD är 2 cm. Kvantitet I: Längden av sidan AB Kvantitet II: 6 cm A I är större än II B II är större än I C I är lika med II D informationen är otillräcklig
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 1 april 2012 01:58:51
	Här: "Geometriska objekt (t ex en triangel) antas vara godtyckligt ritade. Detta betyder att vinkeln på en triangel kan vara större eller mindre än den ser ut att vara. Detta betyder också att en till synes spetsvinklig triangel i själva verket också kan vara trubbvinklig." Se: http://www.df.lth.se.orbin.se/~mikaelb/hprov/11bop/anvisningar-kvanitativdel.pdf. "Illustrationer av geometriska objekt antas vara godtyckligt ritade men värden och beteckningar som ges i illustrationer stämmer alltid. T.ex. kan man i illustrationen nedan se att sidan AC är 5 cm, sidan BC är x, arean är 6 cm2 och vinkeln B är rät. Det framgår däremot inte om sidan AB är längre eller kortare än sidan BC, ej heller om vinkeln A är större eller mindre än vinkeln C." Se figuren i: http://www.studera.nu/download/18.27d86368130216405a6800014454/anvisningar-kvantitativdel.pdf I den uppgiften vi nu diskuterar finns två lösningar beroende på om en vinkel är spetsig eller trubbig. De olika lösningarna gör att man måste svara att man inte har tillräcklig information för att avgöra om I > II eller I
Konversation: Fel i uppgift t. Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 31 mars 2012 23:58:30
	Jag tror att uppgift 12 i XYZ i Kvantitativ del i Provpass 5 på Högskoleprovet vt 2012 är felkonstruerad. 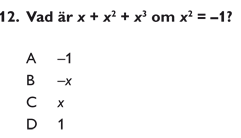, se http://studera.nu/hogskoleprovet/hogskoleprovet/facittillhogskoleprovet.5.328dbf20131f69ece448000337.html. "Dessa konventioner gäller om inte annat anges i den enskilda uppgiften. Alla variabler är reella tal." Se: "Konventioner – Kvantitativ del" i http://www.studera.nu/download/18.27d86368130216405a6800014454/anvisningar-kvantitativdel.pdf. Det finns inget reellt tal för vilket x^2=-1, däremot är x=i eller x=-i komplexa tal som x kan vara. Både x=i och x=-i leder till att x+x^2+x^3=-1. Däremot tror jag uppgiften strider mot konventionen om att x skall vara ett reellt tal om inte annat sägs i uppgiften, fast i och för sig kanske de menar att villkoret x^2=-1 framtvingar komplexa tal. Det är ganska intressant att de kräver Matematik E eller Matematik 2c för att man skall klara Högskoleprovet. De mest populära utbildningarna t.ex. Läkarprogrammet kräver bara Matematik D. Hittills har det inte varit något Nationellt Prov i Matematik 2c och troligen är ingen kurs avslutad. Det vore dock en nackdel för mig om uppgiften ströks ty jag klarade den (m.h.a. komplexa tal).
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 31 mars 2012 14:31:03
	Du har rätt i att 23 och 28 är från fel provpass, men 18 är från rätt och det felet är fortfarande giltigt.
Konversation: Fel i facit till Högskoleprovet pass 5 Kvantitativ vt 2012?
Mikael	Postad: den 31 mars 2012 12:28:48
	Jag tror jag har hittat en del fel i facit till PROVPASS 5 Kvantitativ del 2012-03-31. Det gäller uppgift 18, 23 och 28. Ni får gärna påpeka om jag har fel och i så fall varför. Facit och uppgifterna finns här: http://studera.nu/hogskoleprovet/hogskoleprovet/facittillhogskoleprovet.5.328dbf20131f69ece448000337.html. Provpass 5 - Kvantitativa jämförelser (KVA), 2012-03-31 18. Jag anser att svaret på 18 skall vara D (informationen är otillräcklig) och ej A (I är större än II) som i facit, ty man kan inte anta något om vinkeln vid C. Vinkel C kan t.ex. vara spetsig och då blir II större än I. Det står ju i de allmänna reglerna att man inte får anta något om ej angivna vinklar baserat på mätningar i figurerer. Jag anser att jag har följt reglerna när jag har svarat D. Provpass 5 - Kvantitativa resonemang (NOG), 2012-03-31 23. Jag anser att svaret på 23 skall vara C (Tillräcklig information för lösningen erhålls i (1) tillsammans med (2)) och ej E som i facit, ty a+b+c=27 och a 28. Jag anser att svaret på 28 skall vara B (Tillräcklig information för lösningen erhålls i (2) men ej i (1)) och ej A som i facit, ty 76/16=4.75, d.v.s. tårtan har 5 våningar. (1) räcker ej ty 76-12=64, men 64/16=4 och 64/32=2 och 64/64=1, d.v.s. då kan tårtan ha 5, 3 eller 2 våningar. Provpass 5 - Diagram, tabeller och kartor (DTK), 2012-03-31 Jag har ännu ej kollat dessa uppgifter, men eftersom det är bråttom så har jag skickat detta inlägg till de provansvariga redan nu.
Konversation: Huvudräkningsträningsprogram
Mikael	Postad: den 28 mars 2012 17:53:52
	Nu finns huvudräkningsträningsprogrammet Aritm för CASIO fx-9860GII och kompatibla t.ex. fx-9750GII (men jag har bara testat på den förstnämnda). :lol: Har man inte redan uppdaterat sin grafräknare till senaste OS-versionen (idag är det OS 02.01.0200) så bör man göra det innan man installerar ty annars så fungerar inte Aritm. Skicka filerna med senaste versionen av kommunikationsprogrammet FA-124 (idag 2.00) till grafräknaren utan att börja redigera dem (ty jag har upptäckt att redigering innan framkallar buggar). Filen som skall importeras i FA-124 är ARITM.G1M och den finns här: http://www.df.lth.se.orbin.se/~mikaelb/casio/fx-9860gii/mob-i-l/. Filen innehåller ett huvudprogram och flera underprogram. Man kör programmet ARITM och det är ganska självförklarande. Programmet fungerar på samma sätt som motsvarande för Texas Instruments TI-84 Plus/TI-82 STATS (se tidigare inlägg i tråden). Dock har Casio bredare men lägre skärm och därför har skärmlayouten ändrats. Aritm för Casio är ännu inte noga testat. Tyvärr fungerar inte programmet utan ändringar på äldre Casio grafräknare eftersom det använder Menu och RanInt#, men det skulle kunna ordnas, ty man kan göra en egen meny och ersätta RanInt# med ett uttryck med Ran#. Aritm för Casio är öppen källkod enligt GPLv3+ och får modifieras och spridas i enlighet med denna kända licens. Det kan vara bra att köra huvudräkningsträning innan prov: t.ex. det nu aktuella Högskoleprovet. Här finns förövrigt gamla Högskoleprov: http://www.df.lth.se.orbin.se/~mikaelb/hprov/. :ugeek:
Konversation: Program för polynomdivision på ZX81
Mikael	Postad: den 21 mars 2012 21:03:13
	Polynomdivision ingår i Matematik E, men vissa kanske lär sig det redan i Matematik C. Jag har roat mig med att backporta ett TI-83 BASIC-program för polynomdivision till ZX81 BASIC. Sinclair ZX81 var en hemdator som kom ut 1981 och som i original bara hade 1 KB minne och där minnet dessutom delades av grafikkortet. Grafikkortet delade dessutom på processorn Z80 på ca 3 MHz. Datorn hade bara fyra IC-kretsar i likhet med dagens grafräknare: processor (Z80), ROM (8K - 0,5K för typsnitt), RAM (1K) och en specialtillverkad IC (ULA) för övriga funktioner som tangentbord, ljud och grafik. Polynomdivisionsprogrammet finns även nedan i en 1 KB RAM-version. Polynomdivisionsprogram för ZX81 med 16K RAM (2K räcker nog egentligen): Polynomdivision för ZX81 med 1K RAM: Installerbara program finns en nivå upp: http://www.df.lth.se.orbin.se/~mikaelb/sinclair/zx81/mob-i-l/. ZX81 har nog ökat i popularitet på senare tid eftersom det finns en bra emulator för Android: Zed Ex, http://www.appbrain.com/app/zed-ex-(beta)/org.helllabs.android.zx81. En fördel med denna är att man lätt kan öppna programmen samt utveckla och spara egna som man sedan kan ladda upp. Det finns även ZX81-emulatorer för de flesta andra OS. Programmet för Texas Instruments TI-82 STATS/TI-83/TI-83 Plus/TI-84 Plus finns här: http://tibasicdev.wikidot.com/polynomial-division Programmet för ZX81 blir lite längre eftersom man inte kan redigera listor bekvämt utan måste skriva ett eget inmatnings- och utmatningssystem för dessa. Manualer och litteratur till ZX81 finns som pdf-filer eller ibland som avskrivna till webbsidor, t.ex. http://www.worldofspectrum.org/ZX81BasicProgramming/. Det följde även med en svensk bok som nog finns att låna på bibliotek. För min del var det datorprogrammeringen som gjorde att matematiken blev intressant.
Konversation: Finns mattebok för CASIO FX-CG20 räknare?
Mikael	Postad: den 26 februari 2012 03:28:06
	Att leta efter en mattebok som är anpassad efter en miniräknare låter inte som en så lyckad ide'. En bra mattebok bör knappt nämna miniräknare alls. Varför? Jag tror man kan göra bra matteböcker för en specifik miniräknare. Då kommer instruktionerna och övningarna att fungera exakt. Om du vill veta hur just din miniräknare fungerar så borde det snarare vara en bra manual till räknaren som du borde söka efter. Men manualerna brukar vara för avancerade eftersom de tar upp alla funktioner. Har man en mattebok som är anpassad för en viss miniräknare så går den igenom funktionerna efterhand som de behövs för uppgifterna.
Konversation: Finns mattebok för CASIO FX-CG20 räknare?
Mikael	Postad: den 9 januari 2012 07:38:38
	Jag gjorde en sökning på Libris.KB.se och hittade 20 böcker om Casio. Det är klart att det är bäst om man hittar en bok som är exakt gjord för ens grafräknare, men som reservalternativ kan man välja en som är någerlunda ny och för samma märke eftersom de brukar ha ganska lika användargränssnitt. Det kan också finnas böcker om Casio-miniräknare på kommunala bibliotek som inte finns med i Libris.KB.se. Annars kan du prova att ringa eller e-posta Casio i Sverige och fråga om de har någon bok på gång om just din räknare. Det finns också webbplatser och forum på engelska för Casio-ägare: [list] http://users.telenet.be/gp/casio/ [/] http://www.casiocalc.org/ [/] http://martin.poupe.org/casio/ [/*][/list:u]
Konversation: Att hitta rätt lösningsmetod
Mikael	Postad: den 26 december 2011 05:50:27
	Bra bok om problemlösning på grund- och tidig gymnasienivå: "Liten guide för matematiska problemlösare" (1993, 1997) av Bengt Ulin. Den finns att låna på många bibliotek men kan finnas i magasinet (fråga bibliotekarierna). Den tar även upp typiska högskoleprovsuppgifter. När det gäller träning inför högskoleprovets NOG-uppgifter så rekommenderar jag att man hemma tränar på att lösa uppgiften fullständigt på papper och sedan på provet påbörjar en lösning på provpappret (tillåtet men alla tror kanske inte det) tills man vet vad som är nog med information. Det är också en fördel vid DTK-uppgifterna (diagram, tabeller, kartor) om man kan huvudräkning och överslagsräkning (även där kan man dock räkna med penna på provpappret). Jag har samlat gamla högskoleprov här: http://www.df.lth.se.orbin.se/~mikaelb/hprov/. Jag hade 2.0 på Högskoleprovet. När det gäller matematisk problemlösning i allmänhet kan jag rekommendera "Problemlösning - En handbok i rationellt tänkande" av G. Polya. Originalets titel: "How to Solve It". Vissa exempel i den förutsätter dock differentialekvationer från kursen Matematik E.
Konversation: Rita grafer
Mikael	Postad: den 18 december 2011 15:41:55
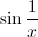
	Nu kan även rita grafer på Google. Här är t.ex. $\sin \frac{1}{x}$ http://www.google.se/search?q=sin(1/x)
Konversation: Trasiga bilder på forumets förstasida
Mikael	Postad: den 16 december 2011 15:39:14
	Det är förstasidan på Forumet som det finns trasiga bilder, d.v.s. http://www.mattecentrum.se/forum/. De två trasiga bilderna syns tydligt i Chrome hos mig och det har varit så länge.
Konversation: Trasiga bilder på forumets förstasida
Mikael	Postad: den 16 december 2011 04:09:40
	Jag har upptäckte för länge sedan två bilder som inte finns och därför visas som trasiga bilder i min webbläsare (Chrome). De finns vid rubrikerna "Regler på forumet" och "Matte E". Besökare kanske drar sig för att göra inlägg i ett forum med trasiga bilder.
Konversation: Huvudräkningsträningsprogram
Mikael	Postad: den 24 november 2011 13:13:41
	Jag utvecklade för ca ett halvår sedan en OpenOffice.org Calc-applikation (d.v.s. motsvarande ett Excel-ark med makron) som tränar användaren i huvudräkning. Det heter Aritm och finns här: http://ooo.orbin.se/. På samma sida finns programmet SpellAlpha som också är skrivet i OpenOffice.org BASIC och också körs i kalkylprogrammet Calc. Det används för att träna bokstaveringsalfabetet som används av civila myndigheter i Sverige. För att köra dem i OpenOffice.org så måste man tillåta osignerade makron som kommer från den egna hårddisken. Programmen bör också fungera i LibreOffice. Det skulle vara ganska lätt att översätta dessa program till Microsoft Excel, och det är fritt fram för andra att göra detta ty programmen är öppen källkod enligt GPL v3+.
Konversation: Wolfram Alpha och formelsamlingar
Mikael	Postad: den 20 oktober 2011 04:01:04
	Android-appar När det gäller formelsamlingar finns det t.ex. Spree Formulas. Jag tyckte dock inte det var så jättebra, ty bl.a. kalkylatorn är meningslös eftersom en formel kan användas på många sätt. När det gäller miniräknare/grafräknare så använder jag oftast Andie Graph. Den emulerar bl.a. TI-83 som är identisk med TI-82 STATS som är mycket populär i skolorna. ROM medföljer inte av upphovsrättsskäl utan det kan man utvinna ur sin egen TI-83 eller annan räknare som stöds av programmet, t.ex. TI-82 (noter att TI-82 ej är så lik TI-82 STATS). Det finns beskrivningar hur man gör detta på ticalc.org. Det är lagligt att använda emulatorn med TI Calculator ROMs om man äger motsvarande miniräknare. Har man ingen TI-83 så kan man ibland köpa en billigt på auktionswebbplatser som Tradera. ROM:en placerar man på valfritt ställe i filsystemet och appen hittar dem när man startar den. Det är ju enkelt för elever om de använder samma miniräknare på telefonen som de får lov att använda på prov. I många skolor finns klassuppsättningar av miniräknare och då bör läraren lagligt kunna dela ut en del ROMs. En nackdel med Andie Graph är att man inte kan importera eller exportera program och data. Det enda man kan göra är att byta RAM-filer.
Konversation: lästal
Mikael	Postad: den 20 oktober 2011 02:29:04
	Jag sökte med Google på fraser ur dina uppgifter och hittade att de två första redan besvarats på andra webbplatser. Att man kan hitta lösningar på webben inte så konstigt eftersom många elever har samma läromedel/kursböcker och de tycker samma uppgifter är svåra. 1. En lösning finns på: http://matteakuten.blogg.se/2010/april/svar-z-rod-uppgift-1018.html. 2. En lösning finns längs ned på: http://www.pluggakuten.se/forumserver/viewtopic.php?id=29942. 3. Hittades ej på webben. Jag tänkte dock också svara på dem om inte någon annan hinner före.
Konversation: Förenkla och skriva i potens form
Mikael	Postad: den 13 oktober 2011 02:47:23
	Det verkar saknas en del i uttrycket t.ex. upphöjt till-tecken (^). Som det står nu blir det 0.
Konversation: Slå på möjligheten att redigera egna poster
Mikael	Postad: den 12 oktober 2011 17:07:48
	På jobbet hade jag inte alternativet "Copy Image Location", så där gick det inte.. Endera har du någon funktionalitet jag inte har när du quotar, eller också klipper du och klistrar vilket jag tycker är lite väl gammalmodigt.. ;) Funktionen som man kan välja när man högerklicka på en bild heter "Copy Image URL" i Chrome. I andra webbläsare kan den heta något annat.
Konversation: Slå på möjligheten att redigera egna poster
Mikael	Postad: den 12 oktober 2011 08:53:47
	Jag tycker det är jättejobbigt att jag inte kan redigera mina poster om det visar sig att jag har råkat skriva fel eller om t.ex. formler i equation editorn visar sig bli felaktiga. Att få tag på den tex-kod jag använt för att skapa fina ekvationer är nästan omöjligt och arbetet med att skriva in dem igen gör att jag snart tröttnar på att använda fina ekvationer. Dessutom skulle jag vilja ha möjlighet att citera andras poster och därigenom kunna kopiera deras tex-kod istället för att vara tvungen att manuellt skriva in den igen när jag ska förklara något. För att få tag på TeX-kod kan man högerklicka på bilden av formeln och välja kopiera länk. T.ex. såg en av länkarna till en formel ut så här: http://latex.codecogs.com/gif.latex?v=\sqrt{v_x^2+v_y^2}. Det som står efter '?' är TeX-koden. Annars kan jag hålla med om att det hade varit lättare om man kunde redigera egna inlägg och citera andras med TeX-kod.
Konversation: vektorer
Mikael	Postad: den 11 oktober 2011 12:34:49
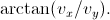
	Jag borde skrivit: Riktningen i grader från norr mot väster får man genom att använda $\arctan(v_x/v_y).$ Hastighet åt väster (Obs!): v_x = 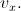Hastighet åt norr: v_y = 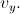Jag skrev v_x & v_y eftersom jag inte orkade använda TeX för att skriva snygga ekvationer med enhetsomvandling då jag inte mindes hur jag skulle göra för att inte enheterna skulle bli kursiverade, men nu vet jag.
Konversation: vektorer
Mikael	Postad: den 11 oktober 2011 09:32:32
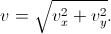
	Man har ingen nytta av s=vt. Man får omvandla 300 km/h till m/s: v_y = 300 km/h = 300 1000/3600 m/s = ______ m/s. Sedan konstaterar man att flygplanet kommer att flyga i någon nordvästlig riktining p.g.a. vinden från öster, v_x = 25 m/s. Med hjälp av Pythagors sats beräknar man farten: $v = \sqrt{v_x^2+v_y^2}.$ Riktningen i grader från norr mot väster får man genom att använda arctan(y/x).
Konversation: Förenkling av rotuttryck
Mikael	Postad: den 11 oktober 2011 08:49:16
	Tackar! Det gick med den metoden. T.ex. tar termer ut varandra och man får även tillfälle att använda konjugatregeln.
Konversation: Förenkling av rotuttryck
Mikael	Postad: den 11 oktober 2011 07:05:37
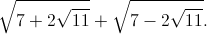
	Jag kommer ej på hur man skall förenkla detta rotuttryck: $\sqrt{7+2\sqrt{11}}+\sqrt{7-2\sqrt{11}}.$ Enligt facit och Wolfram Alpha blir svaret: 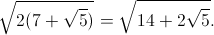$\sqrt{2 (7+\sqrt{5})}=\sqrt{14+2\sqrt{5}}.$ Hur löser man uppgiften steg för steg? Uppgiften finns i boken "Mot bättre vetande i matematik" 3:e upplagan och är där uppgift 1.61f. Den kräver nog bara kunskaper från Matematik 1c.
Konversation: Räcker Matteboken.se som gymnasiematematikbok?
Mikael	Postad: den 30 augusti 2011 05:14:36
	Jag undrar om http://Matteboken.se/ är tillräcklig som matematikbok för gymnasiets kurser. D.v.s. kan en elev som fått G i Matematik B ta sig igenom texterna och filmerna och klara uppgifterna i Mattebokens Matte C-kurs utan andra läromedel än denna efter detta klara minst G på ett verkligt nationellt prov i Matematik C? Är det inte totalt sett för få uppgifter för att få tillräcklig rutin och bredd? Samma fråga men för kurserna Matematik D & Matematik E?
Konversation: Huvudräkningsträningsprogram
Mikael	Postad: den 10 juli 2011 08:31:00
	Nu finns en sorts version av Aritm för Android, se http://www.df.lth.se.orbin.se/~mikaelb/microemu/all.html. Den finns inte på Android Market utan måste hämtas från tidigare nämnda webbplats som apk-fil. Innan man hämtar den måste man kryssa i en ruta om att man vill installera från källor utanför Android Market (Meny/Inställningar/Program/Okända källor) -- normalt sätt är detta förbjudet av säkerhetsskäl. Filen man skall hämta via t.ex. den inbyggda webbläsaren är http://www.df.lth.se.orbin.se/~mikaelb/wap/m_o_b_aritm_midp2_0.apk. Om filen inte installeras automatiskt så kan man leta upp var man sparade den och klicka på den i filhanteraren. Sedan kan man köra appen. Första gången kommer den att fråga om man vill installera J2ME Runner från Netmite.com och då gör man det. Java/J2ME Runner behövs för att denna version av Aritm för Android är automatiskt konverterad från Java-appen. J2ME Runner behöver i sin tur en massa behörigheter eftersom den måste ha alla behörigheter som Java-appar eventuellt kan behöva. Just Aritm använder dock inga av behörigheterna. Aritm-appen fungerar bra min och en del andra Android-telefoner/plattor som jag provat den på.
Konversation: Huvudräkningsträningsprogram
Mikael	Postad: den 24 mars 2011 12:53:50
	Jo, man kan installera det på de flesta Texas Instruments grafräknare som är vanliga. Man kan hämta ner en version för sin räknare via länken ovan till sin dator och sedan får man överföra den med det speciella överföringsprogrammet och kabeln som passar ens räknare. Man kan också hämta programmet på http://www.ticalc.org/archives/files/fileinfo/432/43269.html. I värsta fall kan man också skriva in programmet för hand i miniräknaren. När man väl har det i en miniräknare så kan man överföra det till andra räknare med link-kabeln. Programmet är öppen källkod enligt licensen GNU GPL och man får alltså vidareutveckla det eller översätta det till andra miniräknare om man sprider det nya programmet med samma licens. Jag har tänkt göra en Casio-version och en Android-version men det är fritt för alla att utveckla dessa samt för iPhone. Att det är många nollor i uppgifterna beror på att det tar upp alla uppgifter man behöver kunna för att genomföra räkneuppställningar. Många vet inte hur man räknar med nollor så det är nog bra att de uppgifterna finns med. I en framtida version skulle man kunna ta tiden på svaren och om man svarade extremt snabbt så skulle man kunna ta bort de uppgifterna när man körde programmet nästa gång.
Konversation: Miniräknare - förslag?
Mikael	Postad: den 22 mars 2011 12:56:47
	Vill man köpa billiga miniräknare/grafräknare så rekommenderar jag auktionssajter som http://www.tradera.com/ med sökord "casio fx", "casio cfx", "texas ins", "TI-8" & "sharp el*". Köp några stycken och prova vilken du gillar bäst. Manualer kan man hitta på nätet. Jag har själv mest erfarenhet av TI och tycker en begagnad TI-83 Plus är något av det mest prisvärda man kan köpa ty den kan även köra roliga program från flash-minne (ej att förväxla med Adobe Flash). Jag köpte en sådan på Tradera för 156 kr inkl. frakt. Som ung kanske man inte får handla på Tradera själv men då kanske du kan få hjälp av någon äldre släkting. Det finns även andra auktionssajter men jag tror de har ett mindre utbud på grafräknarsidan. Även Sharp och Casio gör bra räknare men TI har nog ett större community http://ticalc.org/ även om Casio också har ett community. Man får ha räknare med CAS (Computer Algebra System) på de nationella proven i matematik men de lär vara förbjudna på de nationella proven i fysik vilket gör att man kanske inte kan investera i en sådan om man tänker läsa fysik. Dessutom kan skolor förbjuda CAS-räknare lokalt.
Konversation: hemtenta tills imorgon, panik! snabba svar uppskattas..
Mikael	Postad: den 21 december 2010 16:26:32
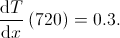
	b) Skulle också kunna skrivas $\frac{\mathrm{d} T}{\mathrm{d} x}\left ( 720 \right )=0.3.$
Konversation: Komplexa tal
Mikael	Postad: den 21 december 2010 16:13:20
	Jag skrev z = a+bi. Då blir z+1/z = a+bi+1/(a+bi). För att detta skall vara reellt så måste imaginärdelen vara 0. Om man förenklar: a+bi+1/(a+bi) = a/(a^2+b^2)+a+(b-b/(a^2+b^2))i. Då skall b-b/(a^2+b^2) = 0, och det är det när b = 0, eller a = -sqrt(1-b^2) eller a = sqrt(1-b^2) samt 1>=b^2 (sqrt betyder kvadratroten). z+1/z är alltså reellt när z = a+b*i har b = 0 eller a = +/-sqrt(1-b^2) och 0

2 Sidor 12>

YAFPro Theme Created by Jaben Cargman (Tiny Gecko)
[Powered by] YAF 1.9.3 RC2 | YAF © 2003-2008, Yet Another Forum.NET
This page was generated in 0,023 seconds.